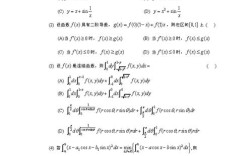考研数学三2025真题在整体难度上适中偏难,题目注重对基础概念的综合应用和计算能力的考查,同时融入了对数学思维和问题解决能力的考察,试卷结构包括高等数学(约56%)、线性代数(约22%)、概率论与数理统计(约22%)三部分,题型涵盖选择题、填空题和解答题,分值分布合理,知识点覆盖全面。

在高等数学部分,重点考查了极限、导数与微分、积分、微分方程、多元函数微分学等核心内容,选择题第1题考查了极限的计算,涉及等价无穷小替换和洛必达法则的综合应用,要求考生熟练掌握各种极限求解技巧;第3题考查了导数的定义,通过分段函数在分段点的可导性分析,考查了对导数概念的深刻理解,填空题第9题考查了二重积分的计算,需要考生根据积分区域的特点选择合适的坐标系和积分顺序,体现了对计算能力的较高要求,解答题题15题考查了多元函数的极值问题,结合了拉格朗日乘数法,要求考生掌握极值的判定条件及实际应用,微分方程部分(解答题题16题)考查了二阶常系数非齐次线性微分方程的求解,涉及特解和通解的求法,强调对基本解法的掌握。
线性代数部分重点围绕矩阵、向量、线性方程组及特征值与特征向量展开,选择题第5题考查了矩阵的秩和向量组的线性相关性,需要考生理解秩的概念及相关性质;第6题考查了二次型的标准形,通过正交变换化二次型为标准形,考查了特征值、特征向量的计算及正交矩阵的构造,填空题第13题考查了行列式的计算,涉及分块矩阵的行列式性质,要求考生灵活运用矩阵运算规则,解答题题20题考查了线性方程组的求解,包含齐次和非齐次方程组的解的结构分析,需要考生掌握基础解系和通解的求法,同时结合矩阵的秩进行综合推理。
概率论与数理统计部分考查了随机变量及其分布、数字特征、参数估计等知识点,选择题第7题考查了随机变量函数的分布,通过分布函数的定义求解,要求考生掌握分布函数的性质;第8题考查了统计量的分布,涉及样本均值和样本方差的分布,要求考生熟悉常用统计量的分布及其性质,填空题第14题考查了矩估计,通过矩估计法求解未知参数,体现了对参数估计基本方法的掌握,解答题题22题考查了二维随机变量的概率分布及数字特征,需要考生掌握联合分布律、边缘分布律及相关系数的计算;题23题考查了区间估计,涉及正态总体参数的置信区间求解,要求考生理解置信区间的概念及构造方法。
整体来看,2025年考研数学三真题注重基础与综合的结合,题目设置既有对基本概念和公式的直接考查,也有多个知识点的综合应用,考生在复习时需注重对基础知识的夯实,同时加强计算能力和综合应用能力的训练,尤其是对重点章节的核心题型要熟练掌握。

相关问答FAQs
Q1:2025年考研数学三真题中,哪些题目难度较高,需要重点突破?
A:2025年真题中,高等数学部分的解答题题15(多元函数极值)、题16(微分方程求解),线性代数的解答题题20(线性方程组求解),概率论与数理统计的解答题题22(二维随机变量分布)和题23(区间估计)难度相对较高,这些题目不仅考查单一知识点,还涉及多个知识点的综合应用,对考生的逻辑推理和计算能力要求较高,建议考生重点练习这些题型,掌握解题思路和常用方法,尤其是拉格朗日乘数法、二阶微分方程求解、线性方程组解的结构分析以及二维随机变量的数字特征计算等内容。
Q2:如何在复习中有效应对类似2025年数学三真题中注重综合能力的题目?
A:应对综合能力题目需要分阶段复习:夯实基础,确保对基本概念、公式和定理的深刻理解,这是综合应用的前提;进行专题训练,将不同章节的知识点串联起来,例如将多元函数微分学与极值问题结合,或将线性代数的特征值与二次型综合练习;总结解题方法,归纳常见题型的通用思路,如微分方程的求解步骤、参数估计的流程等;通过真题模拟训练,熟悉题目难度和考查方式,提升应试能力,注重计算准确性,避免因粗心导致失分。