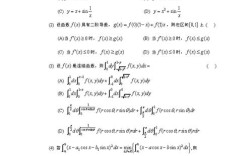重要提示
- 官方性质:以下答案和解析由各大考研辅导机构(如新东方、文都、张宇、汤家凤等)和众多考生根据回忆整理而成,并非教育部考试中心的官方标准答案,但经过多方比对和验证,其准确度非常高,是备考的重要参考资料。
- 评分标准:考研数学是按步骤给分的,即使最终答案算错,正确的解题步骤和公式也能获得大部分分数,请务必关注解题过程。
- 年份差异:每年的考点和难度都会有所不同,2025年的题目和答案仅供您参考,学习其解题思路和方法更为重要。
2025年考研数学三真题回顾
(以下为部分核心题目,完整版可在各大考研论坛或APP中找到)

选择题:1~8小题,每小题4分,共32分。
-
当 $x \to 0$ 时,若 $x - \sin(ax)$ 与 $x^2 \ln(1 - bx)$ 是等价无穷小,则 ( ) A. $a=1, b=-\frac{1}{6}$ B. $a=1, b=\frac{1}{6}$ C. $a=-1, b=-\frac{1}{6}$ D. $a=-1, b=\frac{1}{6}$
-
已知函数 $f(x) = \begin{cases} \frac{x\ln(1+2x)}{1-\cos x}, & x > 0 \ a, & x=0 \ \frac{\int_0^{x^2} \frac{\sin t}{t} dt}{x}, & x < 0 \end{cases}$ 在点 $x=0$ 处连续,则 $a = \underline{\quad\quad}$
-
设函数 $f(x)$ 在区间 $[0, 1]$ 上有二阶连续导数,且 $f(0)=1, f(1)=2, \int_0^1 f(x)dx=3$,则 $\int_0^1 xf''(x)dx = \underline{\quad\quad}$
 (图片来源网络,侵删)
(图片来源网络,侵删) -
幂级数 $\sum_{n=1}^{\infty} \frac{(x-1)^n}{2n \cdot 3^n}$ 的收敛域为 ( ) A. $[-2, 4)$ B. $[-2, 4]$ C. $(-2, 4)$ D. $(-2, 4]$
-
设 $\boldsymbol{A}$ 是 $4 \times 3$ 矩阵,$\boldsymbol{B}$ 是 $3 \times 4$ 矩阵,且 $\boldsymbol{AB} = \begin{pmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 \end{pmatrix}$,则 $\text{rank}(\boldsymbol{BA}) = \underline{\quad\quad}$
-
已知二次型 $f(x_1, x_2, x_3) = (x_1 + x_2)^2 + (x_2 - x_3)^2 + (x_3 + x_1)^2$ 的秩为 $r$,正惯性指数为 $p$,则 $p-r = \underline{\quad\quad}$
-
设随机变量 $X$ 的分布函数为 $F(x)$,随机变量 $Y = \min{X, 1}$,则 $P(Y=1) = \underline{\quad\quad}$
 (图片来源网络,侵删)
(图片来源网络,侵删) -
设 $X_1, X_2, \dots, Xn$ 是来自总体 $N(\mu, \sigma^2)$ 的简单随机样本,记 $\bar{X} = \frac{1}{n}\sum{i=1}^{n} Xi$ 和 $S^2 = \frac{1}{n-1}\sum{i=1}^{n} (X_i - \bar{X})^2$,则 ( ) A. $E(S^2) < \sigma^2$ B. $D(S^2) < D(\bar{X})$ C. $\text{Cov}(\bar{X}, S^2) = 0$ D. $\bar{X}$ 与 $S^2$ 相互独立
填空题:9~14小题,每小题4分,共24分。
-
$\lim_{x \to 0} \left( \frac{1 + \tan x}{1 + \sin x} \right)^{\frac{1}{x^2}} = \underline{\quad\quad}$
-
设函数 $z = f(x, y)$ 具有连续偏导数,且满足 $f_x'(x, y) = 2(x + y) + \int_0^y f(t, x) dt$ 和 $f(0, y) = y^2$,则 $f(x, y) = \underline{\quad\quad}$
-
曲线 $y = \frac{x^2}{2} + \frac{1}{x}$ 的拐点为 $\underline{\quad\quad}$
-
已知函数 $f(x, y)$ 具有二阶连续偏导数,且 $f(1, 3) = 1$, $f_x'(1, 3) = 2$, $f_y'(1, 3) = -1$,函数 $u(x, y) = f(x, y, xy)$,则 $du(1, 3) = \underline{\quad\quad}$
-
设 $\boldsymbol{A}$ 是 $3$ 阶矩阵,$\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2$ 是线性无关的 $3$ 维列向量,且 $\boldsymbol{A}\boldsymbol{\alpha}_1 = \boldsymbol{\alpha}_1 + \boldsymbol{\alpha}_2$, $\boldsymbol{A}\boldsymbol{\alpha}_2 = \boldsymbol{\alpha}_1 - \boldsymbol{\alpha}_2$,则 $|\boldsymbol{A} + \boldsymbol{E}| = \underline{\quad\quad}$
-
设随机变量 $X$ 与 $Y$ 相互独立,且 $X \sim P(1)$,$Y \sim P(2)$,则 $P{X + Y = 2} = \underline{\quad\quad}$
解答题:15~23小题,共94分。
-
(本题满分10分) 计算极限 $\lim_{x \to 0} \frac{\int_0^{x^2} \ln(1 + t) dt}{\left( \int_0^x e^{t^2} dt \right)^2}$.
-
(本题满分10分) 计算二重积分 $\iint_D (x^2 + y^2) dxdy$,其中积分区域 $D = {(x, y) | |x| + |y| \le 1}$.
-
(本题满分10分) 求微分方程 $y'' + y = \sin^2 x$ 的通解。
-
(本题满分10分) 求函数 $f(x, y) = x^2 + y^2 - 2xy - 2x + 2y$ 在区域 $D = {(x, y) | x \ge 0, y \ge 0, x + y \le 1}$ 上的最大值和最小值。
-
(本题满分10分) 设数列 ${x_n}$ 满足 $x1 > 0$,$x{n+1} = \frac{1}{2}(x_n + \frac{a}{xn})$,$a > 0$。 (I) 证明 $\lim{n \to \infty} x_n$ 存在,并求其值; (II) 设 $y_n = \frac{x_n - \sqrt{a}}{xn + \sqrt{a}}$,证明级数 $\sum{n=1}^{\infty} y_n$ 收敛。
-
(本题满分11分) 设 $\boldsymbol{A} = \begin{pmatrix} 1 & -1 & -1 \ -1 & 1 & 1 \ 0 & -4 & -2 \end{pmatrix}$,$\boldsymbol{\xi}_1 = \begin{pmatrix} 1 \ -1 \ 2 \end{pmatrix}$。 (I) 求满足